
How Old is the Earth
A Response to “Scientific” Creationism
by G. Brent Dalrymple

by G. Brent Dalrymple
Other Links:
|
![]() n spite of
conclusive evidence of the Earth’s antiquity, the
proponents of “scientific” creationism stubbornly
maintain that the Earth is only about 10,000 years old (Table 9).
How do they arrive at these numbers? They have no consistent set
of data that leads to any definite age for the Earth. Their
“evidence” consists of invalid criticisms of the
legitimate scientific data, as discussed above, and of some
calculations that supposedly show that the Earth is very young.
These calculations occur throughout the literature of creation
“science” (e.g.,
13, 77,
92, 116,
135), and they have been conveniently tabulated by Morris
(93, 95) and Morris and Parker
(97) (Table 10).
n spite of
conclusive evidence of the Earth’s antiquity, the
proponents of “scientific” creationism stubbornly
maintain that the Earth is only about 10,000 years old (Table 9).
How do they arrive at these numbers? They have no consistent set
of data that leads to any definite age for the Earth. Their
“evidence” consists of invalid criticisms of the
legitimate scientific data, as discussed above, and of some
calculations that supposedly show that the Earth is very young.
These calculations occur throughout the literature of creation
“science” (e.g.,
13, 77,
92, 116,
135), and they have been conveniently tabulated by Morris
(93, 95) and Morris and Parker
(97) (Table 10).
Concerning this tabulation, Morris and Parker (97) make the following statement:
There are, as a matter of fact, scores of worldwide processes which give ages far too young to suit the standard Evolution Model. There are 68 types of such calculations listed in Table I, all of them independent of each other and all applying essentially to the entire earth, or one of its major components or to the solar system. All give ages far too young to accommodate the Evolution Model. All are based on the same types of calculations and assumptions used by evolutionists on the very few systems (uranium, potassium, rubidium) whose radioactive decay seems to indicate ages in the billions of years. As noted in items 25 and 26 in Table I, even these methods (when based on real empirical evidence) yield young ages.
The most obvious characteristic of the values listed in the table is their extreme variability — all the way from 100 years to 500,000,000 years. This variability, of course, simply reflects the errors in the fundamental uniformitarian assumptions.
Nevertheless, all things considered, it seems that those ages on the low end of the spectrum are likely to be more accurate than those on the high end. This conclusion follows from the obvious fact that: (1) they are less likely to have been affected by initial concentrations or positions other than “zero”; (2) the assumption that the system was a “closed system” is more likely to be valid for a short time than for a long time; (3) the assumption that the process rate was constant is also more likely to be valid for a short time than for a long time.
Thus, it is concluded that the weight of all the scientific evidence favors the view that the earth is quite young, far too young for life and man to have arisen by an evolutionary process. The origin of all things by direct creation — already necessitated by many other scientific considerations — is therefore also indicated by chronometric data. (97, p. 251-252; also 95, p. 53-54)
| Age of: | Age (years) | Reference |
|---|---|---|
| Earth | 10,000 | Barnes(13) |
| Earth | 10,000 | Morris (92) |
| Earth | 13,000 | Camping (22) |
| Earth | 10,000 - 20,000 | Kofahi and Segraves (77) |
| Galaxies | nearly 6,000 | Gentry (53) |
| Cosmos | 6,000 - 10,000 | Slusher (116) |
| Earth | 7,000 - 10,000 | Slusher (117) |
The problem with these 68 “ages” of the Earth is that they are all either based on false initial assumptions or have too many unknown variables for a reliable solution, or both. Nearly all these methods have been aired in the scientific literature and found to be so worthless that scientists do not use them for determining the age of the Earth.
An inspection of the reference lists provided by Morris (93, 95) and Morris and Parker (97) shows that most of the calculations were done and published by Morris and his colleagues. Those calculations that are attributed to scientific journals do not actually appear there but, instead, represent unjustified interpretations by creationists of legitimate scientific data.
In addition, Morris (95) and Morris and Parker (97) draw an unwarranted parallel between their calculations and radiometric dating. Most of their “ages” rely on the assumption of constant rates for processes known to vary. Radiometric dating, in contrast, is based on a process (radioactive decay) known not to vary significantly with changes in physical or chemical conditions.
Creationists (e.g., 97) frequently claim that “evolutionists”10 use the principle of uniformity to interpret scientific data, but these authors badly misrepresent the modern meaning of uniformitarianism. The principle of uniformity was developed in the late 18th and early 19th centuries, when geologists finally realized that the rocks and features of the Earth were formed by processes similar to those observable today operating over long periods. This was an important breakthrough in scientific thought because it meant that the Earth’s history could be explained as the result of understandable, natural processes, rather than unknowable, supernatural, catastrophic evens. Creationists, however, typically state or imply that the principle of uniformity, as used by scientists, means that the rates of natural processes are always constant. Hubbert (66) reviewed the principle of uniformity and concluded that it is no longer a useful principle.
History, human or geological, represents our hypothesis, couched in terms of past events, devised to explain our present-day observations. What are our assumptions in such a procedure? Fundamentally, they are two:
(1) We assume that natural laws are invariant with time
(2) We exclude hypotheses of the violation of natural laws by Divine Providence, or other forms of supernaturalism. (66, p. 31)
The principle of uniformity, if it has any meaning at all in modern science, includes no more than these two principles. Indeed, most modern scholars of the subject have concluded that uniformitarianism today is simply the application of the scientific method to nature and that the term is so confusing it should be abandoned (for example, Gould, 59, p. 111). Thus, in assuming and then condemning constant rates for geologic processes, Morris and Parker (97) and their colleagues have set up a straw man based on an obsolete historical definition of uniformity that no modern geologist would accept.
In the remainder of this chapter I examine 49 of the “ages” of the Earth advanced by creation “scientists”, using Morris and Parker’s (97) tabulation (Table 10) as a guide. I will show that all 49 of these ages are invalid and that most are probably best described as silly. I do not discuss the remaining ages listed in Table 10 either because they are not within my area of expertise or because I simply did not have time to investigate them. I think it is reasonable to assume, however, that the 70 percent or so I did investigate are representative and that the methods I do not discuss are likewise meaningless.
Other Links:
|
Barnes (13, 14) claims to have proved that the Earth can be no more than 10,000 years old:
Applying the reasonable premise that this planet never had a magnetic field as great as that of a magnetic star, one can note from Table 2 that the origin of the earth’s magnetic field had to be more recent than 8000 B.C. That is to say, the origin of the earth’s magnetic field was less than 10,000 years ago. Just how much more recent than 10,000 years cannot be determined from present scientific knowledge. If one assumes that the initial value of the earth’s magnetic field were about an order-of-magnitude less than that of a magnetic star the origin would have been about six or seven thousand years ago. (13, p. 25)
Similar statements are made by Morris (92), Slusher (117), and Kofahl and Segraves (77), who cite Barnes (13) as their source.
Barnes’ (13) argument goes like this. The strength of the Earth’s dipole moment has been decreasing linearly since magnetic-field measurements were begun in the early 1800s. This decrease amounts to about 6 percent between 1835 and 1965. Following an hypothesis he erroneously attributes to Sir Horace Lamb, Barnes claims that the magnetic field has been decaying exponentially since the creation of the Earth and calculates that the half-life of the decay is 1400 years. He then extrapolates the decay of the field backward in time until he arrives at the value for a magnetic star, and uses that time (8000 B.C.) to arrive at an upper limit for the age of the Earth.
In another report (33) I show in detail how Barnes’ (13) calculations and conclusions are flawed by false initial assumptions and an overly simplified view of magnetic-field behavior. Thus, it will suffice to summarize briefly the evidence against Barnes’ propositions.
To a first approximation, the Earth’s field is that of a dipole11 with the lines of flux emerging at the poles. On the average, over periods of 100,000 to 1,000,000 years, the magnetic poles coincide with the Earth’s rotational poles. The shape of the dipole field is not ideal but is highly distorted by irregularities superimposed on the dipole field. These irregularities, collectively called the nondipole field, are thought to be caused by eddy currents in the liquid core at the Earth’s core/mantle boundary. Like the dipole field, the nondipole field is slowly and constantly changing. The Earth’s magnetic field we actually observe at any spot on the Earth is the sum of dipole and nondipole fields.
As if this behavior were not complex enough, the Earth’s dipole field does other remarkable things. For example, it occasionally reverses polarity, so that the north pole becomes the south pole and vice versa (30). Paleomagnetic measurements on lava flows indicate that these polarity reversals have occurred at irregular but frequent intervals. Barnes (13) denies that the Earth’s field has reversed, but he fails to cite the relevant literature on the subject and does not refute the numerous observations that prove field reversal.
The field also changes intensity or strength, though not in the way Barnes (13) claims. A careful analysis of the Earth’s field by McDonald and Gunst (85) showed that the decrease in the dipole moment over the past 50 years has been balanced by a corresponding increase in the nondipole component of the field, so that the total energy of the field external to the Earth’s core has been approximately constant. Over the past 120 years, however, it appears that the nondipole-field increase has not been quite sufficient to balance the dipole-field decrease, and so the total field appears to have been decreasing at an average annual rate of about 0.01 percent (129), much less than the value used by Barnes (13). Is there any reason to conclude that this short-term decrease is permanent, as Barnes claims? No. There is conclusive evidence, for example, that the Earth’s field temporarily decays during polarity reversals, which have been frequent during geologic history. Paleomagnetic measurements of the magnetic record in rocks indicate that the Earth’s dipole moment over the past 8000 years or so has not been continuously decaying but, instead, has been fluctuating (Figure 9). How much of this fluctuation is balanced by the nondipole field and how much is a fluctuation in the total magnetic-field energy is not known, but the field certainly does not behave as Barnes (13) claims. Barnes makes the fundamental error of equating the strength of the dipole field with the strength of the total field and, in doing so, ignores the nondipole field, a major component. He also errs in equating the strength of the dipole field with the total-field energy, most of which is probably locked up in a toroidal component internal to the liquid core and, thus, unobservable from the surface of the Earth.
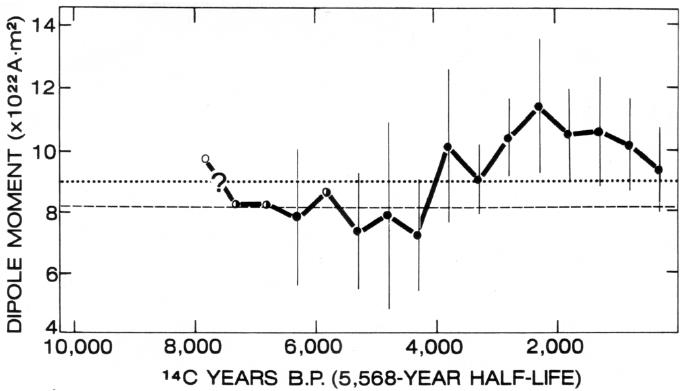
|
The magnetic record in rocks12 clearly indicates that the Earth’s magnetic field during Precambrian times was within about 50 percent or so of its present strength (88). These observations are consistent with theoretical considerations, which show that the Earth’s field is probably generated by a self-exciting fluid dynamo in the Earth’s liquid-metal core and that the necessary energy comes from either radioactive heat within the Earth or gravitational energy, or both. Some time in the future, the magnetic field of the Earth may begin to decrease permanently as the Earth’s available energy is used up, but it will be billions of years before that happens.
The Earth cannot be dated by its magnetic field, and Barnes’ (13) calculations are meaningless, as is his maximum age for the Earth.
Other Links:
|
Morris and Parker (97) list two age calculations based on the influx of meteoritic dust to the Earth (“Too small to calculate”) and the Moon (200,000 years), referenced to Morris (92) and Slusher (116), respectively. Morris (92) argues that the age of the Earth cannot be great because if it were, there would be a thick layer of meteoritic dust on both the Earth and the Moon. Table 11 lists the data he uses. Morris’ values for the density of the dust and the area of the Earth are reasonable, and his slight exaggeration of the age of the Earth is unimportant to this discussion. The real problem is with his value for the influx of meteoritic dust from space, which Morris takes from Petterson (105).
Petterson (105) collected particulate matter from the top of Mauna Loa on the Island of Hawaii, using an air pump designed to sample smog. He analyzed the dust content in a known volume of air for the element nickel. Using a value of 2.5 percent for the nickel content of meteoritic material and assuming that all nickel in the atmospheric dust comes from space, he calculated that about 15 million tons of meteoritic dust falls on the Earth each year. Petterson (105) concluded that his calculation was an upper limit and, after evaluating all the available data, stated that a value of 5 million tons per year was more reasonable. Note that Morris (92) didn’t get Petterson’s upper limit of 15 million tons per year correct and that he completely ignored Petterson’s preferred value.
Although there is probably nothing fundamentally wrong with Petterson’s (105) measurements, his assumptions that nickel is a rare element in the Earth’s crust and in atmospheric dust, and that all the nickel can be attributed to dust from space, are incorrect. More significant is the fact that Petterson’s (105) measurements were made in 1957, the same year that the first satellite was launched. Since the late 1960s, much better and more direct measurements of the meteoritic influx to the Earth have been available from satellite penetration data. In a comprehensive review article, Dohnanyi (39) showed that the mass of meteoritic material impinging on the Earth is only about 22,000 tons per year, a value that would result in a layer only 8.1 centimeters thick in 4.55 billion years (Table 11). Other recent estimates of the mass of interplanetary matter reaching the Earth from space, based on satellite-borne detectors, range from about 11,000 to 18,000 tons per year (67); estimates based on the cosmic-dust content of deep-sea sediment are comparable (e.g., 11, 103). Thus, Morris (92) is off by a factor of more than 600. His conclusion about the thickness of dust on the Moon is likewise in error; he apparently neglects gravitational effects, which reduce the influx per unit area to the Moon by a factor of about 2.
| Creationist version (92) | |||
| Influx of dust to the Earth | 14 × 106 tons/yr | ||
| Density of the dust | 140 lb/ft3 | ||
| Area of the Earth | 5.5 × 1015 ft2 | ||
| Age of the Earth | 5 × 109 yr | ||
| |||
| Scientific version | |||
| Influx of dust to the Earth | 4 × 10-9 g/cm2·yr (20,084 tons/yr) | ||
| Influx of dust to the Moon | 2 × 10-9 g/cm2·yr (2,989 tons/yr) | ||
| Density of the dust | 2.24 g/cm3 (140 lbs/ft3) | ||
| Area of the Earth | 5.10 × 1018 cm2 (5.49 × 1015 ft2) | ||
| Area of the Moon‡ | 1.52 × 1018 cm2 (1.63 × 1015 ft2) | ||
| Age of the Earth and the Moon | 4.55 × 109 yr | ||
| |||
Slusher (116) likewise fails to avail himself of current knowledge on the subject and, instead, uses obsolete dust-influx estimates ranging from 3.6 million to 256 million tons per year. In addition, he advances the erroneous argument that the impact of meteoritic material and radiation from space should have created, by pulverization, a layer of regolith (“soil”) many miles thick if the Moon is 4.5 billion years old.
If a layer, say 0.0004 inch thick of pulverized matter, is formed per year, then, in 10,000 years a layer about four inches in depth would be produced; in 100,000 years a layer of 40 inches; in 1,000,000 years a layer of 3.3 feet; in 4,500,000,000 years a layer about 28 miles in depth would be formed. (116, p. 42)
He apparently fails to realize, however, that once a layer of pulverized material is formed, repeated impacts primarily will stir the existing layer rather than increase its thickness. As Dutch (41) has pointed out, Slusher’s (116) argument is equivalent to arguing that if a farmer plows his field to a depth of 20 centimeters each spring, in 100 years he (and his successors) will have plowed to a total depth of 20 meters.
Considering that good satellite data on meteoritic influx were available before Morris (92) and Slusher (116) published their papers, they obviously have been highly selective in their choice of obsolete data. A more fundamental point, however, is that such calculations are based on faulty premises, including the erroneous assumptions that the meteoritic influx has remained constant for 4.5 billion years and that erosion is negligible, and thus are of no value in determining the age of the Earth or the Moon.
Finally, I have been unable to find the 200,000-year “age of the Earth” based on the accumulation of dust on the Moon (No. 36, Table 10) in Slusher’s (116) paper, nor can I find any data from which this result could have been obtained. Apparently, Morris and Parker (97) have credited Slusher (116) with a calculation that he did not do.
Morris and Parker (97) list an age of 500 million years based on the “influx of magma from mantle to form crust.” This calculation, which appears in Morris (92), is based on the volume (0.2 km3/yr) of lava erupted by Paricutin Volcano in Mexico during the 1940s. Morris (92) notes that intrusive rocks are much more common than lava flows:
… so that it seems reasonable to assume that at least 10 cubic kilometers of new igneous rocks are formed each year by flows from the earth’s mantle.
The total volume of the earth’s crust is about 5 × 109 cubic kilometers. Thus, the entire crust could have been formed by volcanic activity at present rates in only 500 million years, which would only take us back into the Cambrian period. On the other hand, all geologists would surely agree that practically all the earth’s crust had been formed billions of years before that time. The uniformitarian model once again leads to a serious problem and contradiction. (92,p. 157)
But the “uniformitarian model” of which Morris (92) is so critical is a product of Morris (92), not science. He has pulled the value of 10 km3/yr from thin air, assumed that this fictitious rate has been constant over time, and neglected erosion, sedimentation, crustal recycling, and the fact that the injection of magma into the crust is a highly nonuniform process about which little is known. Morris’ (92) calculation is worthless.
This age is referenced to a report by Cook (27), but the calculation was done by Morris (92), using data from Cook’s paper:
Consequently the maximum age of the atmosphere, assuming no original helium in the atmosphere, would be
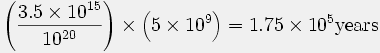
As a matter of fact, Henry Faul (Faul, 1954) has cited evidence that the rate of efflux of helium into the atmosphere … is about 100 times greater than the value used by Cook. This in turn would reduce the age of the atmosphere down to several thousand years! (92, p. 151)
The values in this calculation are the content of 4He in the present atmosphere (3.5 × 1015 g) and the estimated total efflux (1020 g) from the Earth’s crust and mantle throughout geologic time (5 × 109 years). Morris’ (92) calculation is based on the assumption that all the helium released into the atmosphere would be retained, an assumption known to be false.
The helium balance in the atmosphere has been a subject of much study (76). Calculations show that at the present rates of production13, the entire atmospheric content of 4He and 3He could be supplied in about 2.3 million and 0.7 million years, respectively. Various mechanisms are known, however, by which helium escapes from the atmosphere into outer space.
At normal temperatures, the velocity of the average helium atom is less than the velocity required for escape from the Earth’s gravitational field. The elevated temperature in the exosphere, however, increases the kinetic energy of the helium atoms, so that some do escape. Calculations show that this mechanism could account for the escape of about half the 3He produced. Because 4 He is about a third heavier than 3He, however, thermal escape is probably insufficient by a factor of about 40 to account for the loss of 4He. The apparent inadequacy of thermal escape is the basis for Cook’s (27) report and Morris’ (92) calculation, but these authors have overlooked other mechanisms.
The most probable mechanism for helium loss is photoionization of helium by the polar wind and its escape along open lines of the Earth’s magnetic field. Banks and Holzer (12) have shown that the polar wind can account for an escape of 2 to 4 × 106 ions/cm2·sec of 4He, which is nearly identical to the estimated production flux of (2.5 ± 1.5) × 106 atoms/cm2·sec. Calculations for 3He lead to similar results, i.e., a rate virtually identical to the production flux. Another possible escape mechanism is direct interaction of the solar wind with the upper atmosphere during the short periods of lower magnetic-field intensity while the field is reversing. Sheldon and Kern (112) estimated that 20 geomagnetic-field reversals over the past 3.5 million years would have assured a balance between helium production and loss.
Calculations involving the helium balance in the atmosphere are complex because they are sensitive to solar activity, geomagnetic-field fluctuations, the rate of helium production from the Earth, and other factors. Although the helium-balance problem is not yet completely solved, it is clear that helium can and does escape from the atmosphere in amounts sufficient to balance production. The main problem is that the exact roles of the several known mechanisms are unknown. The helium balance of the atmosphere certainly is not a basis for calculating any reasonable estimate of the Earth’s age. Any attempt to do so (92) requires an unjustified oversimplification of a complex problem.
These “ages” are based on some calculations by the creation “scientist” Nevins (99), who used the following basic data:
1) Present influx of sediment to the ocean = 27.5 × 109 tons/yr
2) Present mass of sediment in the ocean = 820 × 1015 tons
3) Present mass of the continents above sea level = 383 × 1015 tons
Dividing (2) by (1), Nevins (99) calculates that all the sediment now in the world’s oceans could have accumulated in 30 million years; dividing (3) by (1), he finds that the present continents could be leveled in 14 million years. From these results, Nevins (99) concludes:
After careful analysis of the erosion of continents and associated sedimentation in the world ocean, we must ask two urgent questions. Where is all the sediment if, as the evolutionist assumes, the ocean is over 1 billion years old? Who has the better model for the ocean — the evolutionist or the creationist? We feel confident that the true answers concerning the origin of the ocean are presented in Scripture. “The sea is His and He made it” (Psalm 95:5). (99, p. iv)
Both the basic assumptions and logic of Nevins’ (99) arguments are wrong. First, he has confused the length of time over which the ocean has existed on the Earth with the ages of the present ocean floors. The existence of abundant Precambrian marine sediment, some more than 3.5 billion years old, clearly demonstrates that the early Earth had an ocean. Some of this earliest sediment contains structures that indicate the presence of algae, and there are undisputed microfossils in sedimentary rocks more than 2 billion years old (26). The Earth, however, is a dynamic body, and the ocean basins are among its youngest features. The floors of the world’s ocean range in age from recent at the crests of midoceanic ridges, where new oceanic crust is forming, to as old as Jurassic (Figure 1) in the parts farthest from the ridges. The sediment in the ocean is practically nonexistent at the ridges and thickens, away from the ridges as the age of the sea floor increases. At the trenches, the sea floors, sediment and all, are being forced down into the mantle where they are consumed to be recycled. Thus, the ocean floors are neither so old nor so passive as Nevins’ (99) calculations presume, and the age of 1 billion years attributed by him to “evolutionists” is of his own invention.
Second, Nevins (99) has assumed constant rates for erosion and sedimentation, processes whose rates have, in fact, varied constantly throughout geologic time.
Finally, Nevins (99) has neglected the fact that the continents are also dynamic and have grown appreciably over time, both by accretion of material at the margins and by addition of material from the mantle below. Uplift, primarily by buoyant and compressional forces, is also a significant factor that tends to offset the leveling effect of erosion.
Thus, the deposition of sediment in the ocean basins and the erosion of continents are parts of a larger, dynamic, and cyclic process that is continually changing the face of the Earth. The mass of sediment in the ocean is not unexpectedly low, nor is the mass of the continents above sea level unexpectedly high. Nevins’ (99) calculations provide no useful information about the age of either the Earth or its ocean.
Morris and Parker (97) present two calculations based on data from a report by Bloch (17), a geologist with the Oklahoma Geological Survey. Using Bloch’s (17) values for the amount of dissolved uranium in the ocean (3.64 × 1015 g), and the present influx of uranium to the ocean (1.92 × 1010 g/yr), Morris and Parker (97) state:
Dividing the first number by the second gives about 189,000 years as the maximum age of the ocean, even with the, very unlikely assumptions that the ocean contained no uranium when it was formed and the river influx was no greater in the past than at present (actually, all the world’s rivers give abundant evidence of carrying much greater flows in the earlier years of their history). The true age would most likely be much smaller than this. (97, p. 249)
Morris and Parker (97) also comment on the possibility that uranium was being removed from the ocean; again, citing Bloch:
However, the old-earth proponent would undoubtedly counter by insisting that much of the dissolved uranium would probably be precipitated out in estuarine or oceanic sediments. Bloch, in fact, has carefully determined the effect of all such possibilities.
A detailed mass-balance calculation for uranium has shown that only about 10% of the present-day river input of dissolved uranium can be removed by known sinks.
That is not all, however.
Low and high-temperature alteration of basalts, organic-rich sediments and co-existing phosphorites on continental margins, metalliferous sediments, carbonate sediments, and sediments in anoxic basins deeper than 200 meters remove about three-fourths of the present-day riverine supply to the ocean.
Since these would seem to exhaust the possibilities, at least 15% of the annual riverine influx of uranium is still available to build up the ocean’s uranium content. Making this allowance, the maximum possible age of the ocean, based on this type of uranium dating, becomes 189,000 + 0.15, or 1,260,000 years. (97, pp. 249-250)
Morris and Parker’s (97) first calculation is made worthless by their assumptions of constant rates of influx and the absence of uranium removal. The second calculation suffers from a more serious flaw: The second quotation from Bloch (17) is incomplete. The next two sentences of Bloch’s (17) statement read as follows:
The remainder can most likely be accounted for by the combined uncertainties in the estimates of U sources and sinks. It appears that the steady state of the world ocean with respect to U can still be maintained in spite of the fact that anthropogenic contributions of this element may be significant. (17, p. 376)
In other words, the uncertainties in the estimates of the rates of influx and removal do not permit Morris and Parker’s (97) conclusion that the uranium in the ocean is not in balance. So far as it known, the amount of uranium in the ocean is in a steady state.
Finally, I should point out that Morris and Parker’s (97) arithmetic is faulty. They apparently have added the 10 percent from the first quotation (which actually is the portion attributable to carbonate sediment and anoxic basins only) to the 75 percent in the second quote to obtain their 15 percent “imbalance.” In Bloch’s (17) report however, the 75 percent value includes all sinks, and so the “remainder” that falls within the uncertainties of the data is 25 percent, not 15 percent.
In addition to uranium, discussed above, Morris and Parker (97) list 31 other “ages” of the Earth based on the influx of various elements and compounds to the ocean via rivers. These ages range from 100 years (aluminum) to 260 million years (sodium) and are cited as evidence for a young Earth:
Similar calculations can be made for all the other dissolved chemicals in the ocean. All will yield relatively small ages (at least in comparison to usual evolutionary estimates of the age of the ocean) but all will, of course, yield different ages. Again, however, even allowing for all realistically possible “sinks,” sedimentation, recycling, etc., none will yield an age anywhere close to the billion-year ages required for evolution.
Attempts to “date” the Earth using the dissolved chemicals in the ocean were common in the late 19th and 20th centuries. Probably the best known example is the calculation by Joly (71) that the Earth’s age is 89 million years, based on the amount of sodium in the ocean. It has been known for many decades, however, that such calculations are wrong because the ocean is in approximate chemical balance, as clearly recognized by Cook:
The validity of the application of total salt in the ocean in the determination of age turned out to have a very simple answer in the fact shown by Goldschmidt (1954) that it is in steady state and therefore useless as a means of determining the age of the oceans. (28, p. 73)
The primary documentation referenced for ages 42 through 68 (Table 10) is the book edited by Riley and Skirrow (108). Neither Morris (92, 95) nor Morris and Parker (97) discuss the calculations that led to these 27 ages, perhaps because there are no such calculations. The values given by these authors are copied directly from a chapter by Goldberg (55) that appears in Riley and Skirrow (108). Goldberg’s (55) Table I is a list of the abundances and residence times of the elements in sea water; it is these residence times that Morris (92, 95) and Morris and Parker (97) give as indicated ages of the Earth. The residence time of an element, however is the average time that any small amount of an element remains in seawater before it is removed, not, as stated by Morris (92), the time “to accumulate in ocean from river inflow,” and has nothing to do with the ages of either the Earth or the ocean. Morris (92, 93, 95) and Morris and Parker (97) have totally misrepresented the data listed in Goldberg’s (55) table. Morris and Parker (97) also reference a paper by the creationist Camping (22), who also confuses residence times with “times to accumulate” and fails to realize that the chemicals in the ocean are basically in a state of dynamic balance.
The documentation cited by Morris and Parker (97) for carbonate, sulfate, chlorine, and calcium (Nos. 15 -18, Table 10) is a book by the creationist author Whitney (132), whose calculations also are meaningless because they suffer from the same inadequacies discussed above.
As I pointed out above, the influx of chemicals into the ocean cannot be used to calculate the age of the Earth because the ocean is in approximate, if not exact, chemical equilibrium. For example, virtually the entire world’s supply of chlorine (Table 10, no. 17) is in the ocean, and nearly all the chlorine carried by rivers is of cyclic origin (55). Chlorine simply evaporates from the ocean, and falls in rainwater either directly back into the ocean or runs into rivers, where it is returned to the sea. Aluminum enters the sea primarily as particulate matter from the weathering and erosion of rocks. It quickly either settles out as sediment or reacts with other elements to form new minerals, and thus has a residence time in ocean water of only about 100 years.
The influx of chemicals to the ocean is an invalid and worthless method of determining the age of the Earth. Morris (92, 95) and Morris and Parker (97) have misrepresented fundamental geochemical data and ignored virtually everything that is known about the geochemistry of seawater.
These “ages” are referenced to the book by Cook (28). I have discussed the flaws in Cook’s (28) reasoning concerning the effects of neutron reactions on lead isotope ratios in a previous section above. I could not find any mention in his book of a similar effect on strontium isotopes, and so how and where Morris and Parker (97) obtained this “too small to measure” age is, at present, a mystery.
The ages of the Earth resulting from these two “methods” are given as “too small to measure,” and the calculation is referenced to Slusher (117). I have read both the 1973 and 1981 editions of Slusher’s monograph several times and cannot find these age-of-the-Earth calculations nor any data from which such a calculation could conceivably be made. Apparently, Morris and Parker (97) have credited their colleague with calculations that he did not do.
The reference for this “age of the Earth” of 5,000 years is a paper by Allen (4) that was originally published in the Bulletin of Deluge Geology and Related Sciences (v. 2, no. 2, p. 37-62) in September of 1942, and reprinted in 1972 in the Creation Research Society Quarterly. Benjamin Allen was a lawyer who for years was the head of the Deluge Society of Los Angeles (4).
Allen (4) reviews the mid-19th century controversy between Charles Lyell, the noted British geologist and close friend of Charles Darwin, and General Andrews Humphreys of the U. S. Army Corps of Engineers concerning the age of the Mississippi River delta. Based on a total sediment thickness of 528 ft, Lyell calculated that the delta and, therefore, the Mississippi River, are 61,000 years old. Adopting the arguments of Humphreys, Allen (4) asserts that only the uppermost 40 ft are delta sediment, and that the underlying sediment is of marine origin. On this basis, he concludes that the Mississippi River and its delta, as well as the other major rivers of the world, originated at the close of the flood 4500 to 5000 years ago. Central to Allen’s (4) thesis is his rejection of the role of subsidence in the accumulation of delta sediment.
There is no disagreement that the present delta of the Mississippi River is relatively young. Recent studies (for example, 58) indicate that deposition began about 18,000 years ago during the last major glaciation when sea level was more than 400 ft lower than at present. Deposition has been rapid, and the sediment reaches a known thickness of 1000 ft. This thickness has been accommodated partly by the rise in sea level following the ice ages and partly by subsidence of the older formations on which the delta was deposited.
Allen’s (4) article is more than four decades out of date, and he draws much of his data and arguments from papers published in the 19th century. Since Allen’s article was first printed in 1942, there have been an enormous number of new data published on the geological history of the Mississippi delta, many of them collected by drilling, and seismic surveys using methods unavailable in the first half of the 20th century. Thus, Allen’s information about the composition, thickness, and age of the delta sediment is incorrect. Allen also ignores the fact that the present delta is but the latest depositational phase in a continuing episode of deltaic sedimentation that began in the Mississippian Period, i.e., more than 330 million years ago (107). Finally, there is absolutely no evidence that either the Mississippi River delta or the deltas of any of the world’s major rivers originated simultaneously during a worldwide catastrophic flood, as Allen (4) proposes.
Even more serious for Morris and Parker’s (97) “age of the Earth” is the simple and obvious fact that the age of the Mississippi River delta does not equal the age of the Earth. Even if Allen’s (4) age of 4500 to 5000 years for the delta were correct, it would still represent only the age of the delta and would not support Morris and Parker’s (97) contention that the Earth is very young. Thus, not only is their “age” of 5000 years for the Earth meaningless, but also their logic defies reason.
This age of the Earth is referenced by Morris and Parker (97) to a report by Wilson and others (133), who estimated the present rate of petroleum seepage into the marine environment at about 0.6 million metric tons per year. The value of 50 million years listed by Morris and Parker (97) as an indicated age of the Earth apparently comes from the following statement by Wilson and others (133):
… the amount of oil available for seepage reflected by these reserve estimates is about 2 × 1014 barrels or nearly 3 × 1013 metric tons. This volume of oil alone could have sustained a seepage rate of 0.6 × 106 years… (133, p. 864)
Morris and Parker (97), however, have chosen to ignore the remainder of the discussion by Wilson and his colleagues:
However, the total oil available for seepage and the time span would be substantially greater since the reserve estimates … include less than half of the offshore area that is considered to be seepage-prone. Moreover, the above reserve figures do not include oil from tar sands and oil shales, which are also potential seepage sources. … (The) inclusion of all potential sources would sustain the seepage rate of 0.6 × 106 metric tons per year for a period of time equivalent to the Tertiary and much of the Mesozoic … when a large percentage of the off-shore oil was being generated. (133, p. 864)
Wilson and others (133) also note that there is no basis for presuming that the seepage rate has been constant and that their calculation was done only to determine whether or not their estimate of the seepage rate is reasonable. Recall that the present ocean basins of the world are relatively young, ranging in age from Holocene to Jurassic. The shelves of the continents, where most off-shore oil is found, also are primarily Mesozoic and younger. Thus, the calculations and conclusions of Wilson and others (133) are consistent with what is known about the age of the rocks in which offshore oil is generated and found.
Morris and Parker (97) have blatantly misrepresented legitimate scientific data and conclusions. The present rate of offshore oil seepage cannot be used to calculate an age for the Earth.
The reference for this age of the Earth is a short news item in Chemical and Engineering News, which, in its entirety, reads as follows:
Plutonium occurs in nature. Dr. Darlean Hoffman and Francine Lawrence at the Los Alamos Scientific Laboratory have chemically isolated about 8 × 10-15 grams of plutonium-224 [sic] from 85 kg. of bastnasite ore from the Mountain Pass, California, mine of Molybdenum Corporation of America. Jack McWherter and Frank Rourke at the Knolls Atomic Power Laboratory, Schenectady, New York, identified the isotope by mass spectrometry. Detection of this relatively short-lived isotope (80 million years) may indicate that synthesis of heavy elements was still occurring at the time of formation of the Solar System. (7, p. 29)
The discovery of natural plutonium-244 was significant partly because it was the heaviest isotope ever found in nature but mostly because it gave scientists a valuable clue about the time of synthesis of the heavy elements. The reasoning is as follows. If the radioactive isotope plutonium-244 was synthesized at the time of formation of the Solar System, then, with a half-life of 80 million years, the 8 × 10-15 g represents the undecayed remainder of 1057 g14, or slightly more than 2 lb — a conceivable amount. On the other hand, if the plutonium-244 was synthesized at the time of formation of the Galaxy, about 12 ± 2 billion years ago, then the original amount would have to be 1.14 × 1031 g or 1.26 × 1025 tons! Thus, the discovery of plutonium-244 in nature suggests that it may have been synthesized as the Solar System formed rather than much earlier.
What Morris and Parker (97) have listed as an 80-million-year indicated age of the Earth is simply the half-life of plutonium-244. Clearly, they do not understand either the content or the significance of the discovery reported in the brief news article they cite as their source of documentation.
This age is attributed to Barnes (14). Barnes (14) summarizes and supports the arguments developed first in 1862 by Sir William Thomson (Lord Kelvin), who calculated that the Earth could be no less than 20 million and no more than 400 million years old (127). Kelvin’s calculations were based on the presumption that the Earth was cooling from an initial white-hot molten state, and his calculations determined how long it would take for the observed geothermal gradient to reach its present configuration. Kelvin also calculated that the Sun is probably no more than 100 million years old and almost certainly no more than 500 million years old (126). These upper limits for the age of the Sun were based on his estimate of the available supply of gravitational energy, which, he concluded, would not last many millions of years longer. Nuclear reactions, which we now know are responsible for the Sun’s fires, were unknown in Kelvin’s time. The value of 24 million years, preferred by Barnes (14) and listed by Morris and Parker (97) as the age of the Earth, is attributed by Barnes to Kelvin but was, in fact, first published by King (73). Lord Kelvin (82), however, agreed with King’s value and adopted it as a likely upper limit for the age of the Earth.
Kelvin and several noted geologists, including Chamberlain (24), feuded over the age of the Earth for more than 35 years because the geologists, basing their estimates on the rates of observable processes, felt strongly that Kelvin’s estimates were much too low. The dispute was resolved in 1903, when Rutherford and Soddy (109) first determined the amount of heat generated by radioactive decay. Rutherford and Soddy readily appreciated the significance of their discovery for cosmologic hypotheses:
It (the energy from radioactive decay) must be taken into account in cosmical physics. The maintenance of solar energy, for example, no longer presents any fundamental difficulty if the internal energy of the component elements is considered to be available, i.e., if processes of subatomic change are going on. (109, p. 591)
Subsequent measurements of the amount of radioactive uranium, thorium, and potassium in the Earth and in meteorites have shown that all the heat flowing from the interior of the Earth outward can easily be accounted for by radioactive decay, although gravitational energy and latent heat of crystallization probably are also important. Barnes (14), in championing Kelvin’s calculations15, states:
Some scientists claim that radioactivity in the earth would alter this limit upward, but none has given any clear analysis of how much it would alter Kelvin’s value. Kelvin was well aware of radioactivity, as is demonstrated by the fact that he wrote several papers on it. That did not appear to him to alter the problem at all. He was working from an actual measured thermal flux gradient and a knowledge of thermal conductivity of the crustal rocks and was still confident that he had shown that the earth’s age does not exceed 24 million years. (14, iii)
The first statement is simply untrue. There is a large volume of literature on the subject of the thermal state and history of the Earth; most beginning geology textbooks treat the subject. The remainder of Barnes’ paragraph also is wrong. Kelvin’s last published remarks on the age-of-the-Earth from cooling calculations were in 1899, four years before Rutherford and Soddy published their findings of the energy available from radioactive decay. While it is true that Kelvin published several papers on radioactivity, these papers were unrelated to his age-of-the-earth calculations. Barnes implies that Kelvin considered the matter and concluded that it was unimportant. In fact, Kelvin privately admitted that his hypothesis regarding the age of the Earth had been disproved by the discovery of the enormous amount of energy available from within the atom (21), although he never recanted. Kelvin apparently realized that he had lost the argument and simply gave up, turning his energies to other matters until his death in 1907.
The pre-20th-century history of the various attempts by scientists and philosophers to estimate the age of the Earth is a fascinating subject that the reader may wish to explore in more detail (1, 48). Probably no estimate caused more controversy than Kelvin’s, and his role in this debate, which lasted for nearly half a century, is the subject of a recent monograph (21). Kelvin’s calculations are interesting from an historical point of view, but for nearly all of the 20th century they have been known to be wrong.
In a recent creationist monograph, Slusher and Gamwell (118) consider the contribution of radioactive heat to the problem of a cooling Earth and conclude that even with radioactivity as a source of heat, the calculations lead to the conclusion that the Earth is young:
The cooling times appear quite small (thousands of years) if the initial temperature of the earth was on the order of that for a habitable planet for any of the models. Even for initial temperatures as high as that for an initially molten earth, the cooling times are vastly less than evolutionist estimates. It would seem that the earth is vastly younger than the old earth demanded by the evolutionists. Thus, the evolutionary hypothesis would seem to be a false hypothesis for explaining things. (118, p. 75)
Their treatment of this important and complex problem, however, is inexcusably naive. They have neglected important sources of heat within the Earth, selected inappropriate depth distributions of radioactive elements, and ignored completely the loss of heat by convection in the mantle. Before discussing the flaws in their conclusions further, I here explain briefly some of the factors that scientists must consider when analyzing the Earth’s thermal history, and review some current thinking on the subject.
The solution to the problem of the Earth’s thermal history consists of an evaluation of the relative importance of both the various sources of heat in the Earth and the several ways in which this heat is transferred from depth to the surface. The problem is complicated by several factors: (1) the early events in the formation of the Earth, many of which would generate large amounts of heat, are poorly understood; (2) the heat generated by radioactivity decreases exponentially over time; (3) the distribution of radioactive elements within the Earth is poorly known; (4) the temperature gradient in the Earth can be measured for only the outer few kilometers; (5) many of the relevant physical properties of the mantle, such as conductivity, specific heat, and viscosity, must be estimated; and (6) the pattern of mantle convection is poorly known.
There are several important sources of heat in the Earth. One is primordial heat, i.e., heat left over from the formation of the Earth. Although the Earth probably accreted cold, radioactivity, gravitational energy from compaction, and segregation of the iron-nickel core probably generated enough heat to raise the temperature of the Earth to near the melting point within 100 to 200 million years of its formation (83, 122). In addition, the heat from impacts of large meteorites during the period when the Earth was still sweeping up large amounts of material from its orbital path generated large amounts of heat and may have resulted in the melting of the outer 100 km or so. Much of this primordial heat has not yet escaped from the Earth.
A second source of heat is radioactivity. This heat is generated by the radioactive decay of uranium, thorium, and potassium contained in the rocks of the Earth. Although the exact distribution of these radioactive elements within the Earth is not well known, there is no problem in constructing reasonable Earth models that attribute most or even all of the heat now flowing outward from the Earth to radioactive decay. For example, all the heat required could be generated by the uranium, thorium, and potassium contained in a granitic crust only 22 km thick (120). Likewise, if we assume that the Earth has a bulk composition similar to that of the primitive meteorites called carbonaceous chondrites, then the heat produced by radioactivity would about equal the present average heat flux from the mantle (119). These two examples, of course, are oversimplifications of a problem of vastly greater complexity, but they do illustrate that radioactivity is probably the single most important mechanism of heat generation in the Earth today. Because radioactive elements decay exponentially over time, radioactive decay would have generated even more heat in the past. For example, 4.5 billion years ago, the rate of heat generation from the decay of uranium, thorium, and potassium in the Earth would have been nearly 6 times the present rate (120).
In addition to primordial heat and heat from radioactivity, contraction of the Earth due to cooling and gravitational-energy release as the core grows may also be important contributors to the Earth’s thermal budget.
Of equal importance as heat sources are the mechanisms by which the Earth loses heat. One is conduction, which involves the transfer of kinetic energy at the atomic and molecular level; this is the same means by which heat is transferred through the bottom of a cooking pan from the burner to the food. The conductivity of rocks, however, is rather poor, and conduction is not particularly efficient. For example, heat generated 4.5 billion years ago at a depth of a few hundred kilometers would just now be reaching the surface if conduction were the only mechanism of heat transfer within the Earth.
The most important mechanism of heat loss from the Earth is convection, which involves the transfer of heat by motion of the hot material itself. Convection is highly efficient and, to a large degree, self-regulating. When a liquid is heated in a pan, for example, the more heat is supplied, the more vigorously the liquid convects, and the faster heat is lost. Calculations show that the rocks of the mantle can be expected to show similar behavior; the more heat is supplied, the less viscous the mantle becomes, the faster it convects, and the more heat is transferred to the surface.
There is little doubt that the Earth’s mantle is convecting. The evidence from continental drift, sea-floor spreading, and the bathymetry of the sea floor is conclusive. Calculations also show that mantle convection is both physically possible and probable. Although at first it may seem impossible for solid rocks to flow, both theory and laboratory experiments show that they can and do, although the mechanism differs somewhat from that involved in the flow of liquid. Estimates of the present rate of mantle convection indicate that the motion is on the order of a millimeter or so per year.
Studies of the thermal budget of the Earth consist of balancing the various heat sources against heat loss through convection and conduction, taking into consideration what is known about the history and physical properties of the Earth. Current studies indicate that of the total geothermal heat flux of 38 × 1012 W, about 63 percent or 24 × 1012 W is lost from the mantle. Only 24 percent (9 × 1012 W) is lost from the continental lithosphere, and perhaps 5 × 1012 W may be lost from the core by plumes of hot material rising from near the core-mantle boundary (122).
The heat flow per unit area from the continents is about the same as from the oceans, although both local and regional variations occur. Because the continents cover only about a quarter of the Earth’s surface, about three-fourths of the total heat flow is through the ocean basins. Virtually all the heat lost from the ocean basins comes from the mantle and is brought close to the surface by convection. About 30 percent of the total global heat loss is at the midoceanic rises, where new crust is forming by the injection and eruption of magma (83, 113). Although conduction plays a role in transferring some heat through the oceanic crust, convection is the dominant mechanism bringing heat from depth. In contrast, heat loss from the continents is primarily by conduction. Of this heat, about two-thirds is generated by radioactivity within the continents themselves (121); the remainder is brought to the base of the continental lithosphere from the mantle by convection, where it is then conducted to the surface. Thus, both convection and conduction play roles in the Earth’s thermal budget; however, on a global scale, most of the heat lost from the Earth is through the ocean basins, primarily by convection in the mantle.
Although radioactivity is probably the dominant source of the heat flowing from the Earth’s surface, some of the heat may be primordial. Recent studies (for example, 113, 119, 122) indicate that the Earth may be cooling at a rate of 5 to 6°C per 100 million years and that primordial heat may constitute 30 to 40 percent of the heat now being lost from the Earth.
What, then, of the conclusion of Slusher and Gamwell (118) that consideration of the Earth’s heat budget indicates that the Earth is very young? They have reached this conclusion by ignoring most of what is known about the chemistry, physics, and history of the Earth. First, they begin with the erroneous assumption that the only heat-loss mechanism for the Earth is conduction; they completely ignore convection. This assumption would be excusable only had their paper been written before the mid-1960s, before there was sound evidence that the Earth’s mantle was convecting.
Second, Slusher and Gamwell (118) seemingly are unaware that the Earth’s surface includes both continents and ocean basins, each of which have different compositions, distinct physical characteristics, and participate in global plate tectonics in quite different ways. They take no account of the differences in either heat generation or loss between these vastly different regimes of the Earth.
Third, they use inappropriate depth distributions for the radioactive elements. Only by adopting the unrealistic assumption that most radioactive isotopes are concentrated in the outer 10 km or so of the crust do their analyses yield cooling times of “thousands of years” rather than millions of years. Although it is true that uranium, thorium, and potassium tend to be enriched in the Earth’s crust, there is every reason to think that the mantle also contains these elements; their concentrations may be small, but the mass of the mantle is so great that significant heat production results.
Finally, thermal analysis of the Earth cannot yield an estimate of its age. The age of the Earth, determined independently by radiometric dating, is one of the boundary conditions that must be satisfied in such an analysis; it is not a result. There are simply far too many things about the history and interior of the Earth that are poorly known and must be estimated. For example, even before convection was known to be an important factor in heat loss from the Earth, scientists were able to devise reasonable thermal models for the Earth that attributed all the heat generated to radioactive decay and all the heat lost to conduction. This was done simply by choosing reasonable distributions and concentrations of radioactive elements that yielded a balance between generation and loss and preserved the observed geothermal gradient. As new knowledge about mantle convection and the early history of the Earth accumulated, these models were changed to account for the new findings. There is as yet no definitive thermal model for the Earth, and it is absurd to expect that any such model can be used to determine the Earth’s age. Thus, the supposed determination of the Earth’s age from thermal calculations by Slusher and Gamwell (118) is totally without merit.
Morris and Parker (97) list an age of the Earth of 5 million years based on the accumulation of calcareous ooze on the sea floor. The reference for this age is a report by Ewing and others (45)16. The report by Ewing and his coworkers describes a study of the sediment distribution on the Mid-Atlantic Ridge. They found that the sediment there is quite thin and concluded that at the present rate of sedimentation, the sediment could have accumulated in about 2 to 5 million years. This short time was puzzling to them because the ocean basins were then thought to be very old — their report was published before the theory of plate tectonics and sea-floor spreading was formulated, tested, and confirmed. We now know that the midoceanic ridges are very young and still active; in fact, their age is zero at the ridge crests. The 2 to 5 million years calculated by Ewing and his coworkers is about right for that part of the ridge surveyed by them. Note that Ewing and his coworkers did not calculate an age for the Earth, nor did they produce or describe any data with which such a calculation could be made.
Morris (93, 95) lists an “indicated age of Earth” of 100,000 years from “formation of carbon-14 on meteorites”; he references a report by Boeckl (18). Boeckl’s report, however, was about tektites, not meteorites. Tektites are small globules of glass whose origin has been the subject of much debate but is now thought to be from meteoritic impacts on the Earth. Boeckl (18) was attempting to establish a cosmic-ray-exposure-age for these objects to determine their residence time in space. To do so, he assumed a terrestrial age for the tektites of 10,000 years to make his calculations. Boeckl did not calculate an age for the Earth, nor did he produce any data that could be used to do so; Morris (93, 95) even has the number wrong. It is interesting to note that this “age” does not appear in the recent list of Morris and Parker (97) (Table 10), and so perhaps even they realize its absurdity.
10 “Evolutionist” is a term used by creationists to include all scientists who disagree with them.
11 A dipole is a magnet with one north and one south pole. A simple bar magnet is one type of dipole.
12 Barnes (13) asserts that this record is unreliable, but he is wrong again. I have refuted Barnes’ claim on this matter in detail in another paper (33).
13 4He comes from the decay of uranium and thorium in rocks, whereas 3He is primordial. Both are “produced” by escaping from the crust and mantle into the atmosphere.
14 Remember that radioactive decay is exponential, so in calculating back to the original amount of plutonium, the quantity doubles every 80 million years.
15 It is curious that Barnes does so. Lord Kelvin thought that the Earth was millions of years old, a view contrary to that of Barnes and his creationist colleagues (Table 9).
16 Morris and Parker cite the Bulletin of the Geophysical Society of America, but there is no such organization; it is the Geological Society of America.
‡ Note
by Jon Fleming, 2005: Dalrymple’s figure for the area of
the Moon is four times larger than it should be; apparently
someone used the diameter instead of the radius in the area
calculation. The final result, a 4.1 cm thick layer on the Moon,
is not affected by this error. Since his area of the Earth
(5.5×1015 ft2) is
correct, his yearly influx per square centimeter on the
Moon (2×109
g/cm2/year)
is also correct.
[2×109
g/cm2/year×4.55×109 years]/(2.24 g/cm3) = 4.1 cm

| Home Page | Browse | Search | Feedback | Links |
| The FAQ | Must-Read Files | Index | Creationism | Evolution | Age of the Earth | Flood Geology | Catastrophism | Debates |